Examples of Nominal Data Examples of Continuous Data
If you do not see the menu on the left, please click here.
A definition
For statistical analysis, we think of data as a collection of different pieces of information or facts obtained from counts, measurements or experiments to draw conclusions, to answer a research question or just have an idea of what is going on regarding a particular issue [1] .
These pieces of information or facts are called variables. A variable is an identifiable piece of data containing one or more values [2] . Those values can take the form of a number or text (where sometimes text can be converted into numbers).
At DSS we deal primarily with numeric data in electronic form.
The general format of numeric data depends on the following:
· Storage. The software use to manipulate it and, therefore, to store it.
· Trait. The quantitative or qualitative trait of each piece of information or variables.
The storage
These are some of the storage types:
1. ASCII. This is the most universally accepted format that most programs recognize. It stands for "American Standard Code for Information Interchange". We can think of ASCII data as data ready for analysis [3] . Practically any program that deals with numeric data can open these types of files. It can have two forms:
· Delimited format where each variable is separated by a comma, tab, space or any special character. The extensions of these files are usually *.csv, *.txt, *.prn, *.data, etc.
· Explicit or record form (fixed) where variables are structured in certain way. You will need the file structure of the data to write a program to read it. The format of these type of data can varied: *.dat, *.txt, *.raw, etc
An example of *.CSV (comma-separeated-value) dataset

An example of tab separated dataset (can have extension *.txt, *.dat, *.data, etc.)
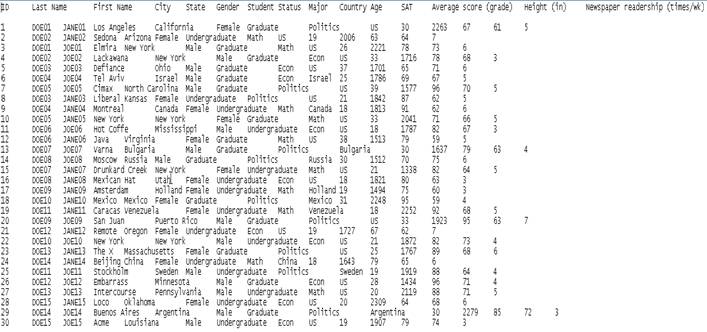
An example of space separated dataset (*.prn, *.txt)
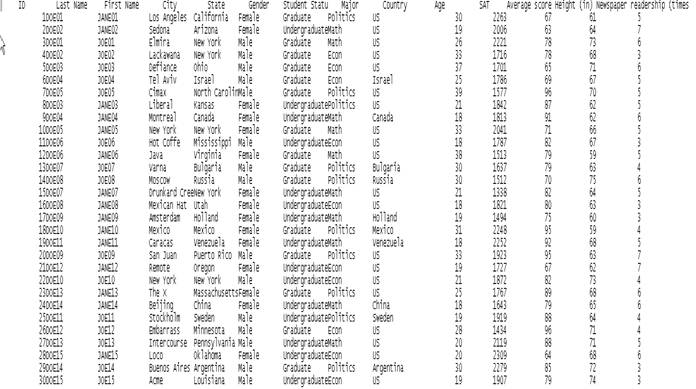
An example of a text dataset (*.txt, *.dat)
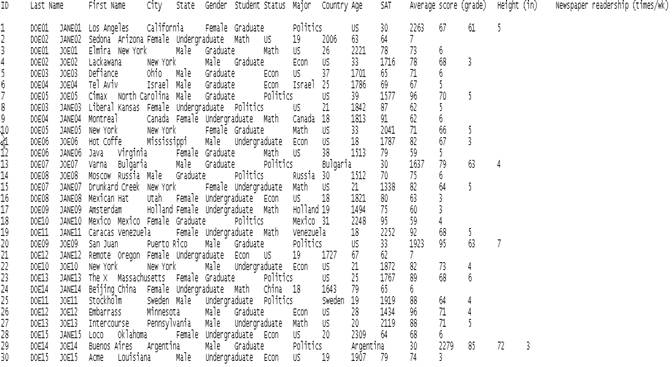
An example of plain text data (*.raw, *.txt)
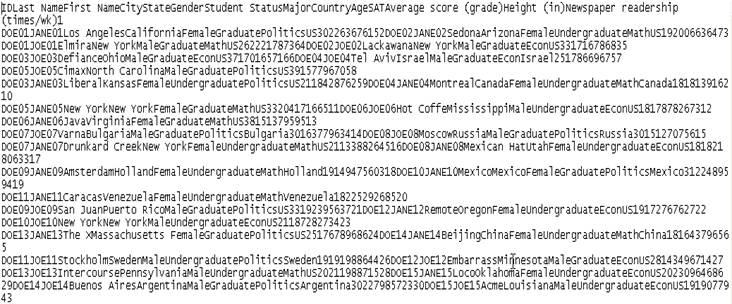
1. Excel , spreadsheet format with extension *.xls (Excel 2003 or earlier versions), *.xlsx (Excel 2007). Columns represent variables, rows represent observations.
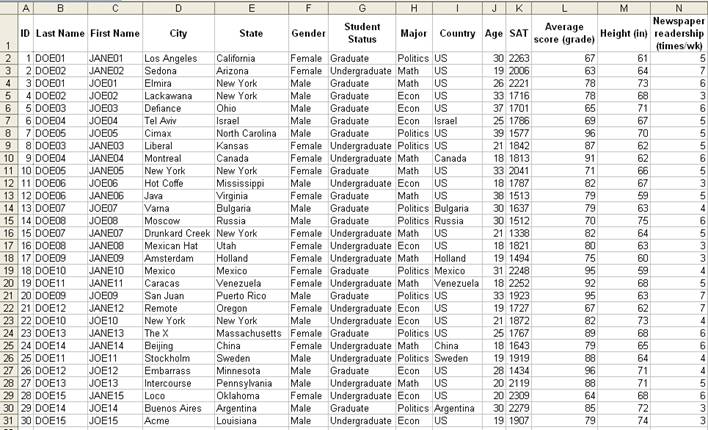
2. Stata, statistical software with extension *.dta. The extension of the file read ASCII data is *.dct (dictionary file). Program files have extension *.do. Columns represent variables, rows represent observations.
3. SPSS, statistical software with extension *.sav, *.por. Program files to read and to process data have extension *.sps. Columns represent variables, rows represent observations.
4. SAS, statistical software with extension *.sas7bcat, *.xpt. Program files have extension *.sas.
5. MATLAB, mathematical modeling and data analysis software with extension *.m
For a comprehensive list of formats see:
http://whatis.techtarget.com/file-extension-list-M/0,289951,sid9,00.html
The trait
Numeric data can have two different traits: qualitative or quantitative [4]
Qualitative
A qualitative trait defines the categories that provide some meaning to the numerical value. In reality this value is just a label. Data with some qualitative trait are called categorical data. There are two types: nominal and ordinal. Descriptive statistics for this type of data are in the form of percentages or proportions. We find the type of data mostly (but not limited to) public opinion, surveys or census data.
Here is an example for this kind of data, in a recent New York Times article:
"A study of nearly 4,000 men and women from
In men, keeping quiet during a fight didn't have any measurable effect on health. But women who didn't speak their minds in those fights were four times as likely to die during the 10-year study period as women who always told their husbands how they felt, according to the July report in Psychosomatic Medicine. Whether the woman reported being in a happy marriage or an unhappy marriage didn't change her risk."
[The New York Times, Health section, web edition, October 2, 2007, link: http://www.nytimes.com/2007/10/02/health/02well.html?_r=1&oref=slogin ]
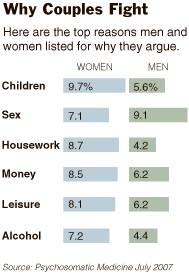
Source: The New York Times, Health section, web edition, October 2, 2007
http://graphics8.nytimes.com/images/2007/10/01/health/1002-sci-sub2WELL.gif
Nominal data
The qualitative trait sex defines in general two categories: females and males. These could be represented by the numbers 1 (females) and 2 (males), or any other numbers or order. This type of data is called nominal, in particular, binary since it has only two categories.
Nominal data can also be non-binary (more than two categories). Let's say we are interested in color preferences, so the qualitative trait is color. Here we could have more than two categories: black, white, green, blue, red, etc. Which could be represented by the numbers 1, 2, 3, ,4, etc.
For nominal data numerical values are just a representation of the label without any actual numerical property. In the color example, 2 is not necessarily greater than 1 nor is double than 1. Likewise, 1 is not lower than 1 nor is half of 2. No arithmetic operation can be performed with this type of data. They are just labels however this does not prevent them to be used for statistical analysis (as binary or dummy variables).
Ordinal data
For ordinal data order matters. Examples: freshman, sophomore, junior, senior, etc; level of agreement: strongly disagree, disagree, agree, strongly agree (this is known as the Likert scale). You can label these responses as 1, 2, 3, 4, 5, etc. but unlike nominal data order provides some meaning to the numbers: they go from negative to positive, from low to high, from younger to older, from less frequent to more frequent, or viceversa. Like nominal data the numbers just represent labels without any numerical properties. There is no indication that the difference between seniors and juniors is greater or lower than the difference between juniors and sophomores. In the same way no arithmetic operations can be performed here but there are some ways to use them for complex statistical analysis.
Quantitative
A quantitative trait produces numerical data from some sort of counting method or measurement device. There are two types of numerical data: discrete and continuous. Descriptive statistics for this type of data summarize location (i.e. the mean or average, median, mode) and variability (standard deviation, variance, etc.)
Discrete
Discrete data is generally the result of some sort of counting, showing some gaps between values. For example students, general population, number of cases, number of reports, number of books cataloged, etc. In the image below, what do you see between number 1 (ducky) and number 2 (bunny)? Well, you see nothing; there is some empty space in between, there is a gap between number 1 number 2.

Continuous
Continuous data is generally the result of measurements. For example, same question, what do you see between number 1 and 2? There is no empty space! No gap, there is something in between, usually more numbers. So, with continuous data there is always a value between any two, no gaps.

Examples are time, height, distance, size, temperature, financial returns, etc.
In the same way as categorical, continuous data have two groups: interval and ratio. Interval data has a specific order and equal intervals (a $5 difference could be from $1 and $6 or $10 and $15). Ratio in addition to be interval it has a natural zero like income where 0 means "not money at all". Temperature on the other hand is only interval data since 0 indicates temperature and not the lack of. In practice, the distinction between interval and ratio does not make much of a difference.
Some controversy…
When doing data analysis, data taxonomy can be a problem and for some it is actually irrelevant. Sometimes and in some cases categorical variables can be treated as continuous when the sample size is large enough; continuous data can also be converted to categorical and analyzed accordingly (like income brackets or age categories). As homework read the following article and draw your own conclusions.
http://www.spss.com/research/wilkinson/Publications/Stevens.pdf
References and useful links
Kachigan, Sam, Statistical analysis : an interdisciplinary introduction to univariate & multivariate
methods .
Data levels and measurement http://www2.chass.ncsu.edu/garson/PA765/datalevl.htm
Types of Data http://www.stat.psu.edu/~resources/ClassNotes/ljs_04/sld018.htm
Introduction to Categorical Analysis http://www.socialresearchmethods.net/tutorial/Cho/intro.htm
Categorical data http://www.stat.yale.edu/Courses/1997-98/101/catdat.htm
Bloomberg Financial Glossary http://www.bloomberg.com/invest/glossary/bfglosa.htm
Forbes Financial Glossary http://www.forbes.com/tools/glossary/index.jhtml
Political Glossary http://www.politicalglossary.net/
A Glossary of Political Economy Terms http://www.auburn.edu/~johnspm/gloss/
Elections Glossary http://www.pbs.org/elections/glossary/index.html
Glossary of Social Science http://www.faculty.rsu.edu/~felwell/glossary/Index.htm
duronforkabounce80.blogspot.com
Source: https://www.princeton.edu/~otorres/Data101/Data101.htm
0 Response to "Examples of Nominal Data Examples of Continuous Data"
Post a Comment